A Painless Guide to Cryptography for Zero-Knowledge Proofs

Wrestling with cryptography concepts is a rite of passage for every developer who wants to learn about zero-knowledge proofs (ZKPs). If you’re anything like me, you probably fell right into the deep end when talk of “finite fields,” “generators”, and the “Diffie-Hellman Exchange” came up.

Consider this your life raft! Now that I’ve gotten the hang of things, I’d like to save you as much time as possible. In a previous post, we covered the basics of modular math. Building on those concepts, we can now go deeper into the fundamentals of cryptography and how they work in ZKPs.

By the end of this post, you’ll be in great shape to understand how zkSNARKs work under the hood. That said, it’s important to remember that this is purely introductory. I encourage you to further explore these topics on your own. As you’ve probably learned in your training to become a developer, that’s the only way these concepts will “click”.

Let’s Start with Finite Fields

It sounds technical, but don’t let the name intimidate you. Finite fields are pretty much what they sound like — a set (or “field”) of limited (or “finite”) elements, like numbers. The number of elements is called the cardinality, or order, of the field. The number of elements in a finite field will always be a power of a prime number. For instance, a finite field can have 2, 3, 4 ($2^2$), 5, 7, 8 ($2^3$), 9 ($3^2$), 11, 13, 16 ($2^4$), etc., elements.

You should also know about closure. This helpful principle states that the result of any arithmetic operation performed on elements within a field will stay within the field. Why is that possible? Because all operations are performed modulo the cardinality of the field. In other words, the result of any arithmetic operation in a finite field is reduced modulo the cardinality to ensure that the result remains within the field's defined set of elements.

As for addition, subtraction, multiplication, and division operations within a finite field (excluding division by zero), they all follow the properties you’re familiar with from regular arithmetic, such as associativity, commutativity, distributivity, and the existence of additive and multiplicative identities and inverses.

Ok, I know I just threw a lot at you. Let’s see this in action in a few examples.

Arithmetic Operations in a Finite Field

Let's consider the finite field $\mathbb{F}_7$, which includes the elements {0, 1, 2, 3, 4, 5, 6}. We can see that this is a field of order 7 (which is, of course, a prime number).

How would we perform arithmetic operations on this finite field?

Addition

4 + 6 = 10. But 10 isn’t in $\mathbb{F}_7$, which breaks the closure principle requiring all elements to be within the field. That’s why we use the modulus operation (you can read my primer on modulus here). Since the result is 10, we do modulo 7. Therefore, 4 + 6 = 10 mod 7 = 3, which is in $\mathbb{F}_7$.

Subtraction

2 - 5 = -3. But negative numbers aren't in our field. To resolve this, we do -3 modulo 7, which would be 4. So, 2 - 5 = -3 mod 7 = 4, which is in $\mathbb{F}_7$.

Multiplication

3 $\times$ 4 = 12. Again, 12 isn’t in $\mathbb{F}_7$, so we compute 12 mod 7, which gives us 5. Thus, 3 $\times$ 4 = 12 mod 7 = 5 in $\mathbb{F}_7$.

Division (or Multiplicative Inverse):

For division, we multiply by a number’s multiplicative inverse (to understand why, see the modulo post). The multiplicative inverse is the number that gives a product of 1 when multiplied by the given number. For example, the multiplicative inverse of 3 in $\mathbb{F}_7$ is 5 because 3 $\times$ 5 = 15, and 15 mod 7 = 1.

So, to compute 4 divided by 3, we need to multiply 4 by the multiplicative inverse of 3, which is 5, as shown above. Therefore, 4 / 3 = 4 $\times$ 5 = 20 mod 7 = 6, which is in $\mathbb{F}_7$.

Additive and Multiplicative Identity

Additive Identity

The additive identity is the element that doesn’t change its value when added to any element in the set. In most number systems and finite fields, that number is 0.

For example, using the same finite field of $\mathbb{F}_7$ above, if we add 0 to any element, the value doesn't change:

1 + 0 = 1 (mod 7)

2 + 0 = 2 (mod 7)

3 + 0 = 3 (mod 7)

4 + 0 = 4 (mod 7)

… and so on

Therefore, 0 is the additive identity in $\mathbb{F}_7$.

Multiplicative Identity

Likewise, the multiplicative identity is the element that doesn’t change its value when multiplied by any element in the set. In most number systems and finite fields, 1 is that number.

Using the same finite field $\mathbb{F}_7$ as above:

0 $\times$ 1 = 0 (mod 7)

1 $\times$ 1 = 1 (mod 7)

2 $\times$ 1 = 2 (mod 7)

… and so on

Therefore, 1 is the multiplicative identity in $\mathbb{F}_7$.

Additive and Multiplicative Inverses

Additive Inverse

The additive inverse of an element is a number that, when added to the element, equals the additive identity (which is 0, as we saw above).

In the finite field $\mathbb{F}_7$ ({0, 1, 2, 3, 4, 5, 6}), the additive inverse of 4 is 3 because 4 + 3 = 7, and 7 mod 7 = 0.

Similarly, the additive inverse of 3 is 4 (because 3 + 4 = 7 mod 7 = 0), the additive inverse of 2 is 5 (because 2 + 5 = 7 mod 7 = 0), and so on.

Multiplicative Inverse

The multiplicative inverse of an element (except for 0) is a number that, when multiplied with the element, results in the multiplicative identity (which is 1, as we saw above).

Using the finite field $\mathbb{F}_7$ again, the multiplicative inverse of 3 in $\mathbb{F}_7$ is 5 because 3 $\times$ 5 = 15, and 15 mod 7 = 1.

Similarly, the multiplicative inverse of 2 is 4 (because 2 $\times$ 4 = 8 mod 7 = 1), the multiplicative inverse of 4 is 2 (because 4 $\times$ 2 = 8 mod 7 = 1), and so on.

Associativity, Commutativity, and Distributivity

Associativity

Associativity means that when you perform the same operation on three or more numbers, you can group them in any way, and the result will be the same. This holds for both addition and multiplication.

For example, (3 + 4) + 2 = 7 + 2 = 9 mod 7 = 2 (mod 7). If we rearrange how we group the numbers where we put 4 and 2 in parenthesis instead of 3 and 4, we will get the same result: 3 + (4 + 2) = 3 + 6 = 9 mod 7 = 2. Therefore, (3 + 4) + 2 = 3 + (4 + 2) in $\mathbb{F}_7$.

The same thing is true for multiplication. (3 $\times$ 4) $\times$ 2 = 24 mod 7 = 5. If we rearrange 3 $\times$ (4 $\times$ 2) = 3 $\times$ 8 = 24 mod 7. So, (3 $\times$ 4) $\times$ 2 = 3 $\times$ (4 $\times$ 2) in $\mathbb{F}_7$.

Commutativity

Commutativity means that changing the order of the numbers doesn’t change the result. For example, 3 + 4 = 7 mod 7 = 0 and 4 + 3 = 7 mod 7 = 0. Therefore, 3 + 4 = 4 + 3 in $\mathbb{F}_7$.

It works for multiplication as well. For example, 3 $\times$ 4 = 12 mod 7 = 5 and 4 $\times$ 3 = 12 mod 7 = 5. Therefore, 3 $\times$ 4 = 4 $\times$ 3 in $\mathbb{F}_7$.

Distributivity

Distributivity means that if you have a number multiplied by the sum of two other numbers, you can "distribute" the multiplication over each of the two numbers inside the parentheses.

For example, 3 $\times$ (4 + 2) = 3 $\times$ 6 = 18 mod 7 = 4. Also, (3 $\times$ 4) + (3 $\times$ 2) = 12 mod 7 + 6 mod 7 = 5 + 6 = 11 mod 7 = 4. Therefore, 3 $\times$ (4 + 2) = (3 $\times$ 4) + (3 * 2).

Ok, But Why Do Finite Fields Matter?

That was a lot of math and definitions, I know, but hopefully, it wasn’t too difficult to follow. So, why did I make you understand all of that? Well, finite fields are incredibly useful in cryptography because, by working with a finite set of elements, you gain quite a few advantages, such as:

• No overflow or underflow errors since we’re working with a finite set of elements
• More efficient computations because we use a fixed number of elements and thus a fixed memory size
• More challenging discrete logarithm problems, which is a fundamental assumption for many cryptographic systems, as we’ll see later

But that's enough of finite fields. Let’s move on to generators.

Generators

In cryptography, generators are elements in a group (e.g., a finite field) that can generate all other elements in that group through repeated application of a group operation. They produce a sequence of distinct values that loop back to the initial element.

Let's look at an example. Suppose we have a finite field $\mathbb{F}_7$, where the order is 7, and we have a generator, g, which is 3.

Using the generator, we can compute all of the elements of the finite field $\mathbb{F}_7$ like this:

$g^0 ≡ 3^0 ≡ 1 (mod 7)$

$g^1 ≡ 3^1 ≡ 3 (mod 7)$

$g^2 ≡ 3^2 ≡ 2 (mod 7)$

$g^3 ≡ 3^3 ≡ 6 (mod 7)$

$g^4 ≡ 3^4 ≡ 4 (mod 7)$

$g^5 ≡ 3^5 ≡ 5 (mod 7)$

$g^6 ≡ 3^6 ≡ 1 (mod 7)$

$g^7 ≡ 3^7 ≡ 3 (mod 7)$

As you can see, applying the generator g repeatedly to different powers yields all the elements in the group modulo 7. In this case, the group contains the elements {1, 2, 3, 4, 5, 6}.

Moreover, repeating this process “wraps around to” the initial element — We can see in the above example that $3^6$ is 1 mod 7, so we looped back to 1, then 3,and so on. Pretty neat, huh? And useful too. After all, generators pop up in various cryptographic protocols because of their use in the discrete log problem. Speaking of…

What’s the Discrete Log Problem?

Imagine we have a prime number, p, and a generator, g. We then generate y by raising g to some unknown exponent x and take the remainder modulo p. It’d look like this:

The “discrete logarithm problem” asks us to find the unknown exponent x when given the generator value g, the prime modulus p, and the value y. In other words, we want to determine the exponent x that satisfies the equation.

This might seem simple at first glance, but it becomes very challenging when the values of g, p, and x are large. There’s no known efficient solution to do this. The only way to find x is by brute force.

The security of many cryptographic algorithms relies on the assumption that solving the discrete logarithm problem is computationally infeasible within a reasonable timeframe. In other words, even with powerful computers, it would take an impractical amount of time to find the value of x if given the values of g, p, and y.

Diffie-Hellman Exchange

Let’s look at an example of a cryptographic protocol that relies on the discrete log problem — the Diffie-Hellman exchange. The Diffie-Hellman key exchange lets two parties, let’s call them Alice and Bob, establish a shared secret key over an insecure communication channel.

Here's how it works:

Setup

• Alice and Bob agree on a large prime number, p, and a generator, g, within the finite field
• The prime number p and the generator g are publicly known and shared between the two people

Key Generation

• Each person independently generates a private key:

  • Alice chooses “a” as their private key
  • Bob chooses “b” as their private key

• The private keys are randomly selected from the range [1, p-1] and kept secret.

Public Value Exchange

• Each person calculates a public value by raising the generator g to their private key modulo p:
  • Alice → $A = g^a (mod p)$
  • Bob → $B = g^b (mod p)$
• The public values A and B are shared with each other over the insecure channel.

Shared Secret Key

• Alice and Bob calculate the shared secret key by using their own private key and the public values from the previous step:
  • Alice computes shared secret key $K = B^a (mod p)$
  • Bob computes shared secret key $K = A^b (mod p)$
• The K values that Alice and Bob generate are the same
• Hence, they were able to generate a shared secret key without needing to send it across the wire

Diffie-Hellman Exchange

The security of the Diffie-Hellman key exchange above relies on the computational hardness of the discrete logarithm problem: Given the public values A and B, it’s infeasible for an attacker to determine the shared secret key K. In other words, if an attacker has access to g, p, and A, they can’t compute a or b because the discrete log problem is hard to solve.

Discrete Log Problem

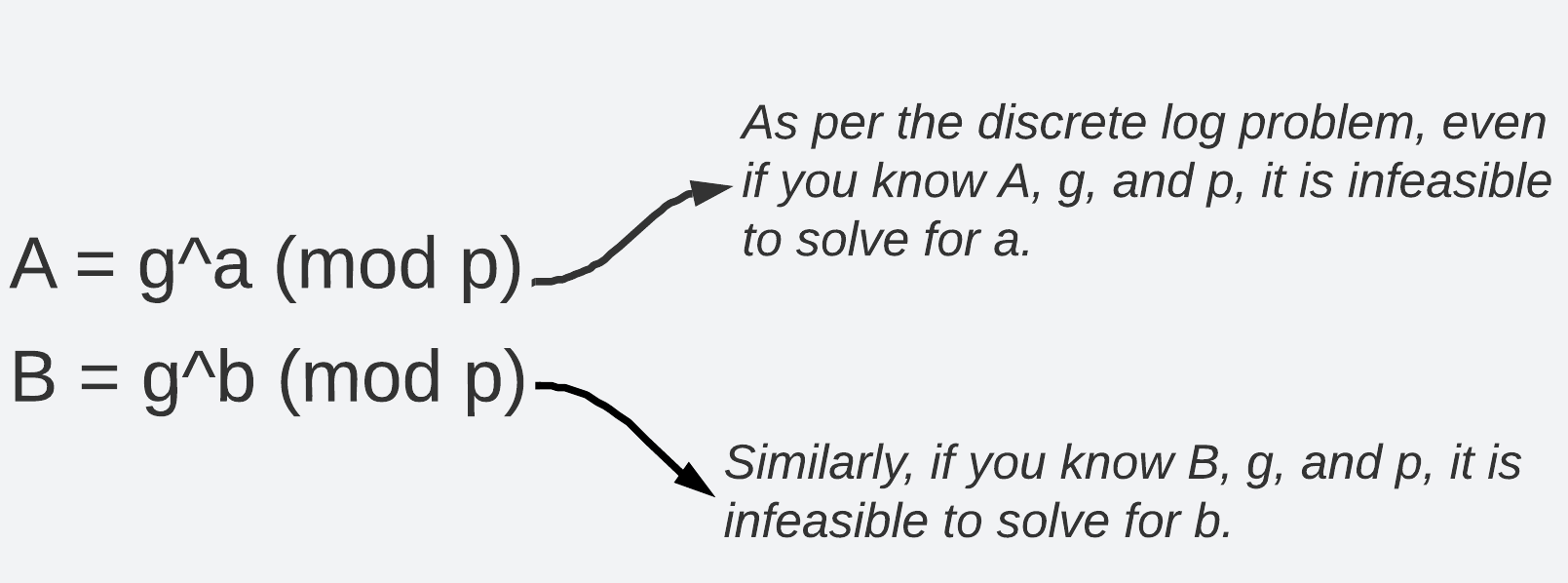
How are Generators Useful for Zero-Knowledge Proofs?

One primary reason we use generators to construct ZKPs is simple — they let us do arithmetic on encrypted polynomials (e.g., add two encrypted polynomials) without decrypting them. This lets us do computations on encrypted data while preserving the privacy of the underlying values.

In other words, it’s key to the “zero knowledge” part of ZKPs! Alright, onto our final topic: Elliptic Curve Cryptography.

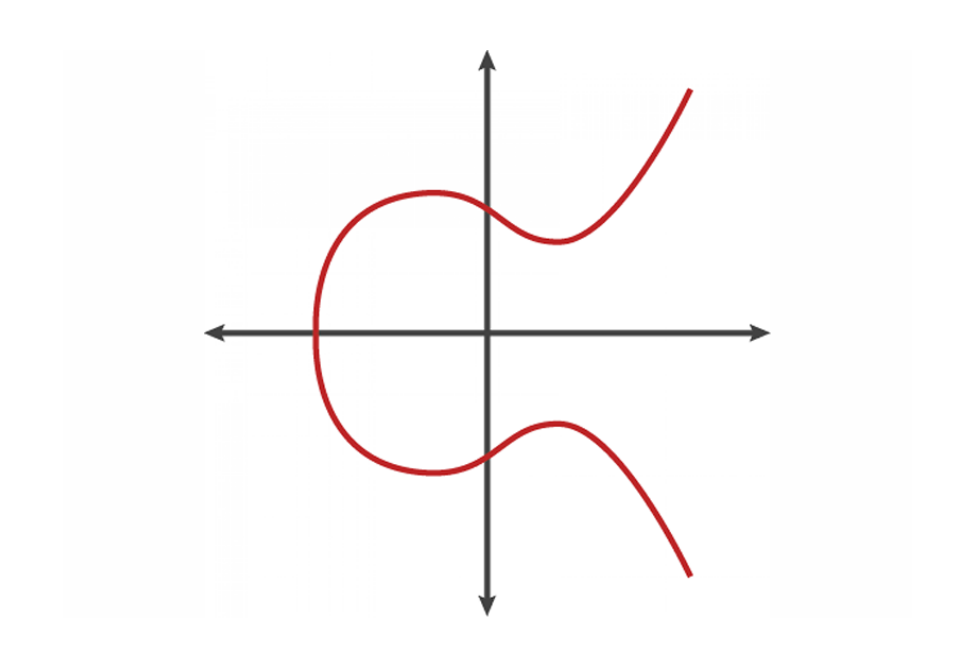
Elliptic Curve Cryptography (ECC)

Take a look below. This is a mathematical curve with a unique shape called an “elliptic curve.” This elliptic curve has unique properties that make it useful for cryptography.

Elliptic Curve

In Elliptic Curve Cryptography (ECC), we work with points on the elliptic curve. These points have coordinates (x, y) that satisfy a specific equation: $y^2 = x^3 + ax + b$, where 'a' and 'b' are constants that define the curve.

Points on Elliptic Curve

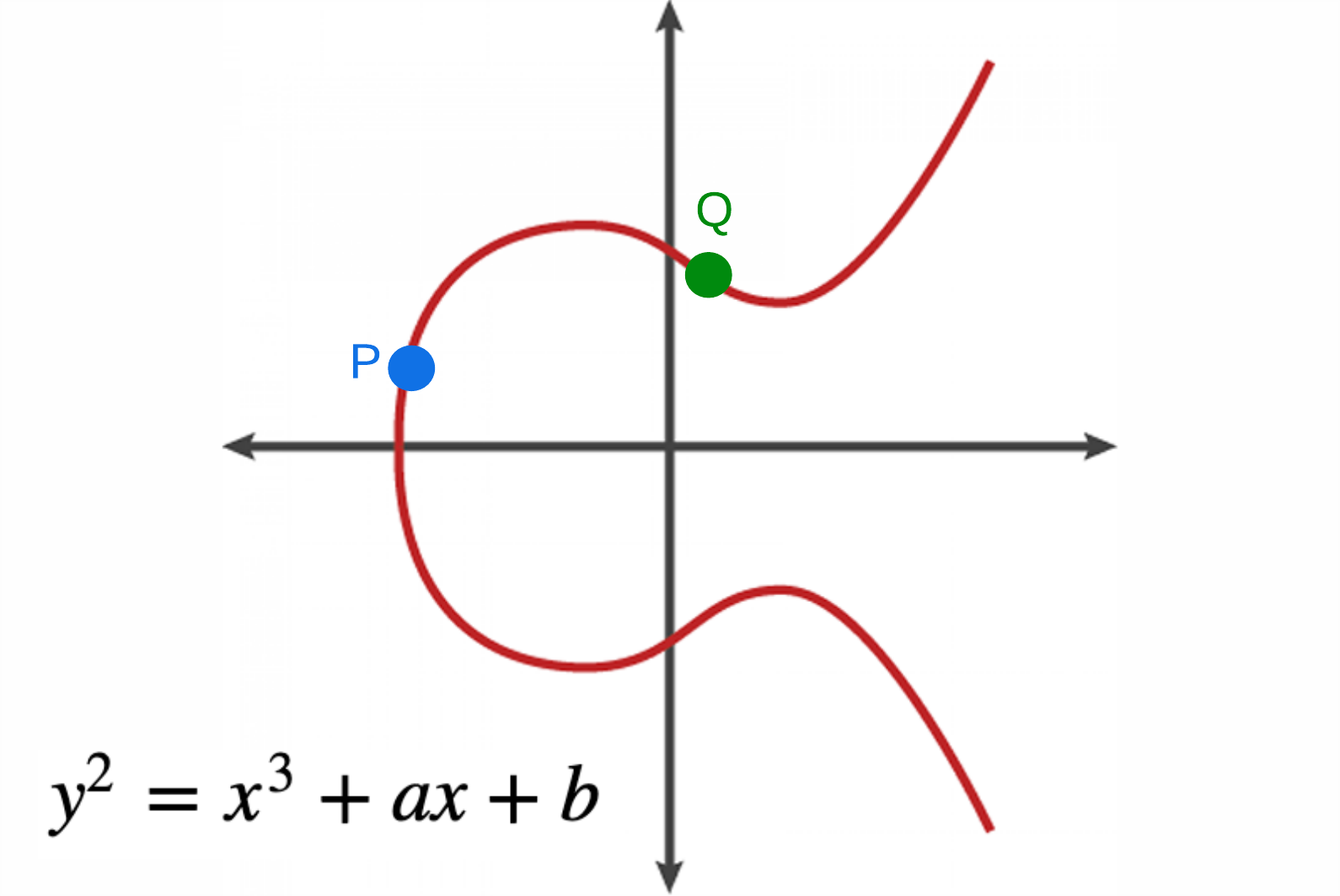
ECC uses points on the curve to perform cryptographic operations. Let’s take a look at a few of these operations below.

Infinity

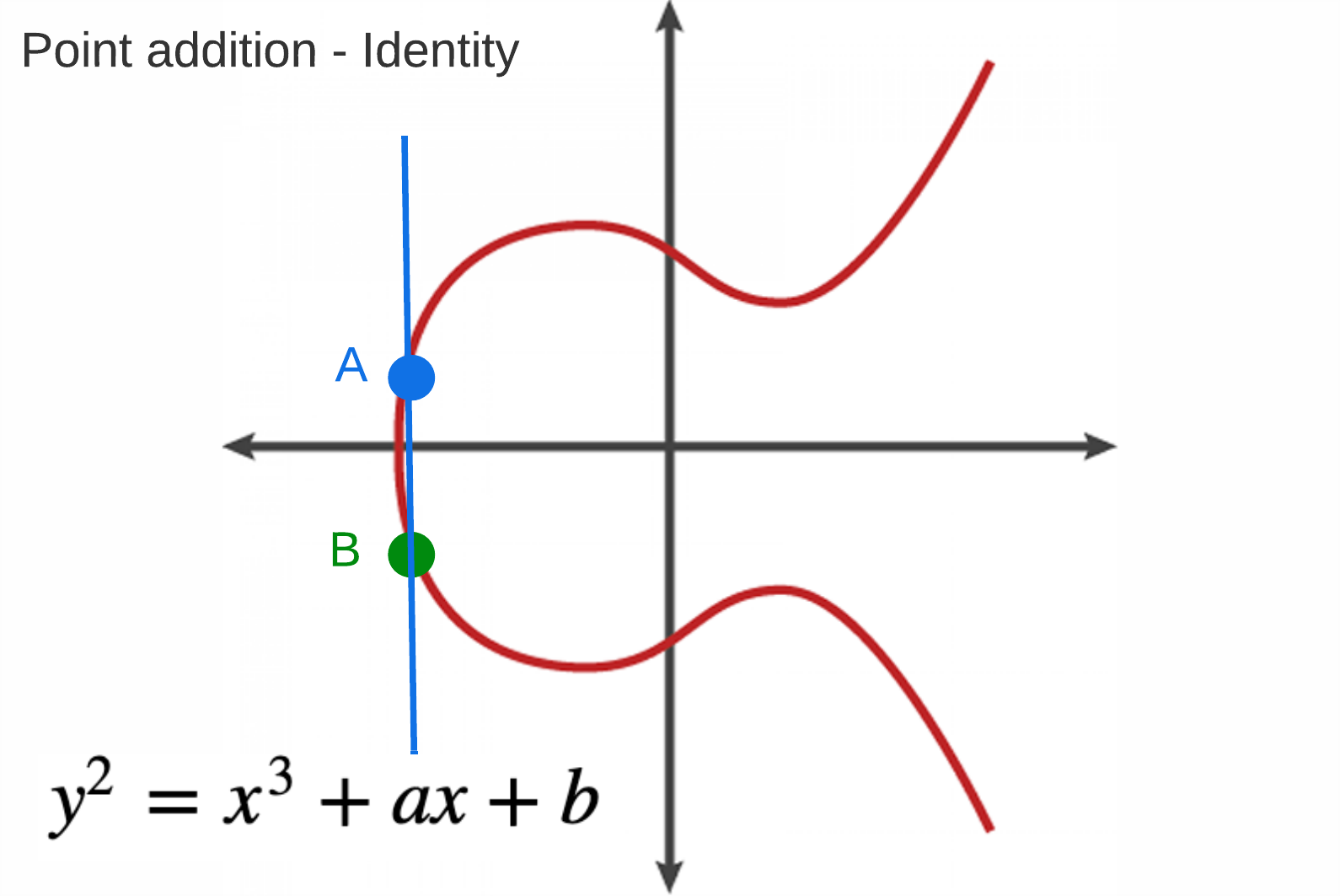
0 is called the identity element. Adding 0 to any other point on the curve equals that other point, including infinity itself.

• 0 + P = P
• 0 + 0 = 0

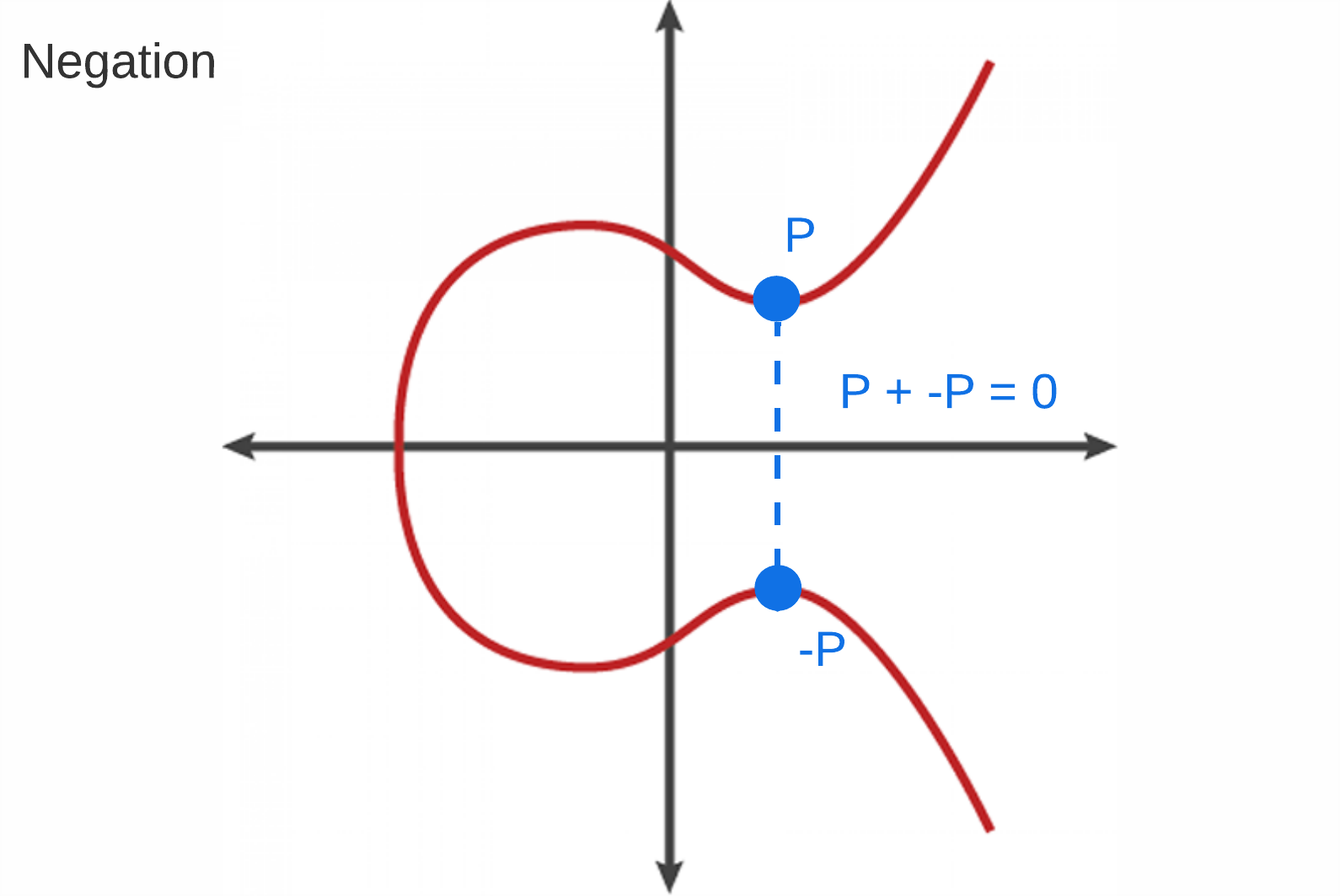
Negation

Negation refers to finding a point on the curve where adding it to itself will result in a point at infinity.

• P + (-P) = 0

Point Negation

Addition

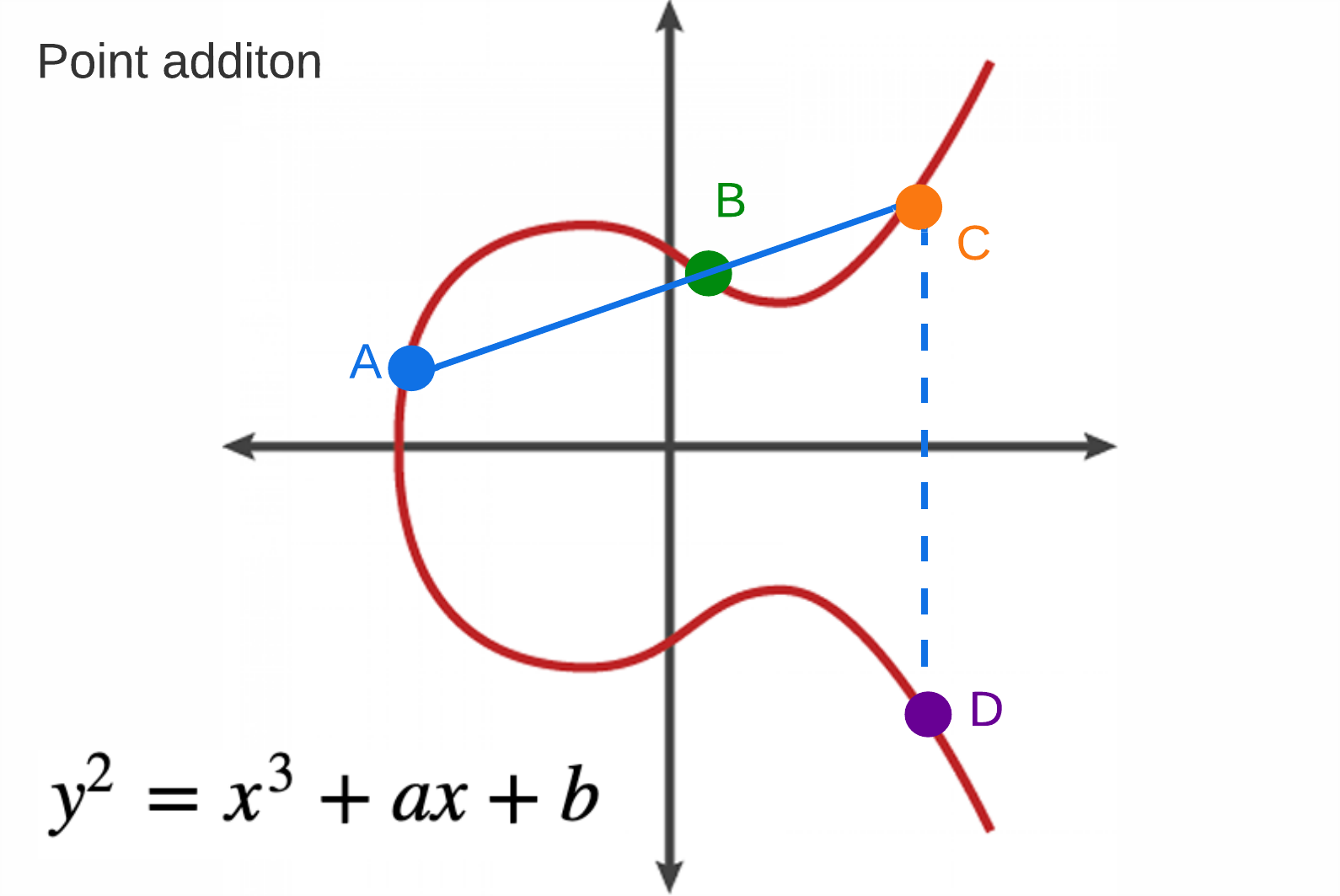
Imagine we want to add two points, Point A and Point B, on an elliptic curve.

• First, draw a straight line connecting Point A and Point B
• Extend this line until it intersects the elliptic curve at a third point, which we'll call Point C
• Reflect Point C across the x-axis, and this is the sum of Point A and Point B

Point Addition

Point Addition - Identity

Point addition has two useful properties:

• Commutative: Adding points in any order results in the same point:

  • P + Q = Q + P
  • P + Q + R = R + Q + P = P + R + Q

• Associative: Rearranging the parentheses in an expression will not change the result:

  • (P + Q) + R = P + (Q + R)
  • P + P + P + P + P = (P + P) + (P + P) = 2P + 2P = 4P
  • P + P + P + P + P + P + P = (P + P + P + P) + (P + P) + P = 4P + 2P + P = 7P

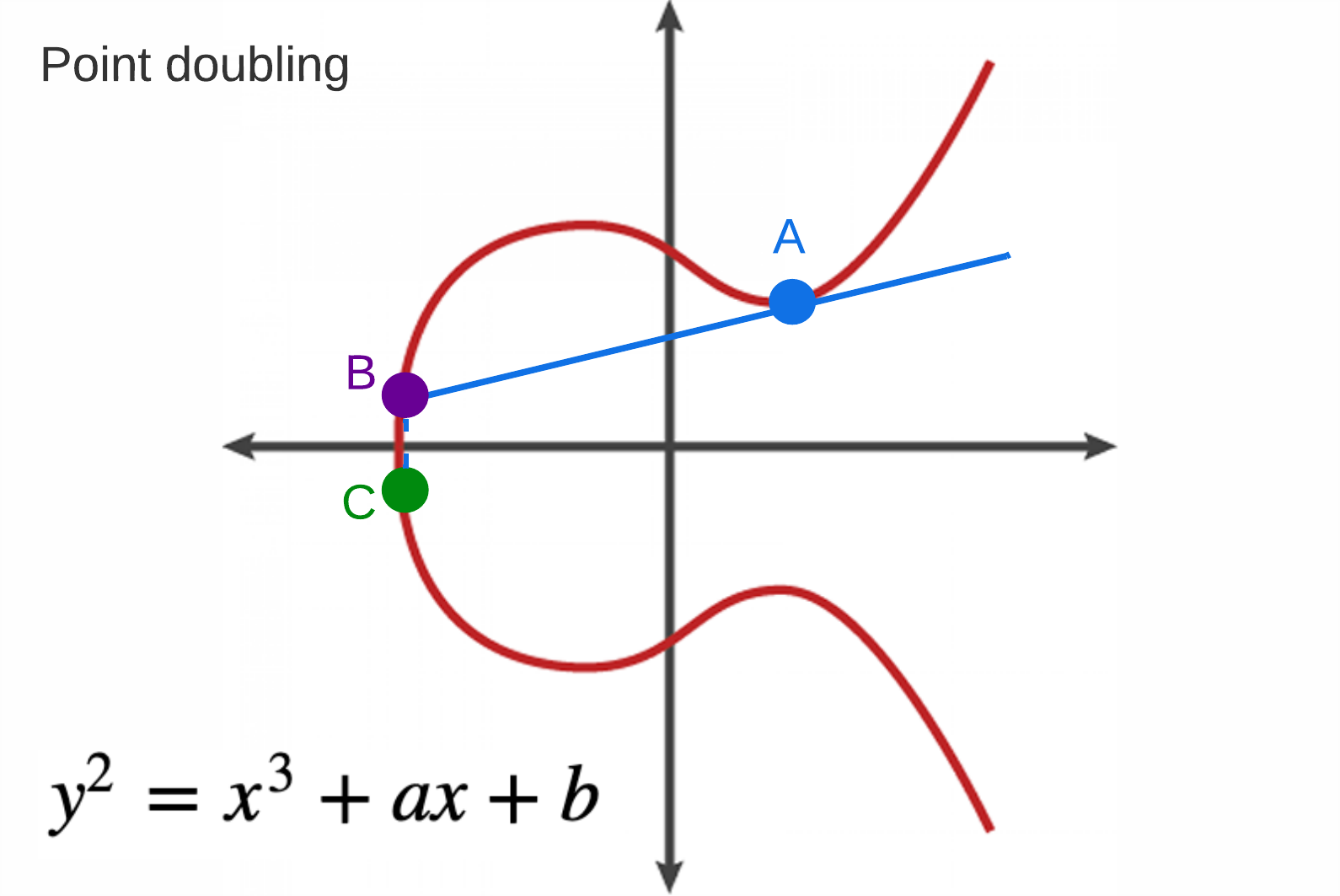
Doubling

Point doubling is a special case of point addition where both points are the same. Imagine we have a point, Point A, on an elliptic curve, and we want to add it to itself.

• To do so, we first draw a tangent line to the curve at Point A
• Next, extend this line until it intersects the curve at a second point, Point B
• Reflect Point B across the x-axis to obtain the resulting point, which is the doubling of Point A

Point Doubling

Scalar Multiplication

The most common operation is called “scalar multiplication,” which is at the core of many cryptographic protocols and algorithms based on ECC. Scalar multiplication is where a point on the curve is multiplied by a secret number called a scalar.

Recall that an elliptic curve has the equation $y^2 = x^3 + ax + b$, where 'a' and 'b' are constants. On this curve, we have a specific point called the base point, P.

Now, imagine we have a scalar, which is just a regular number — let's say 5. In scalar multiplication, we repeatedly add the base point P to itself several times, determined by the scalar value.

So, to perform scalar multiplication with a scalar of 5, we start with the base point P and add it to itself four more times:

1P + 1P + 1P + 1P + 1P = 5P

To see it in action, you can watch this animation:

Finally, let’s talk about an important property relevant to all of the operations mentioned above. Under this property, the resulting point will always be another point on the same curve. This gives rise to the Elliptic Curve Discrete Log Problem (ECDLP), which we’ll discuss next.

Elliptic Curve Discrete Logarithm Problem (ECDLP)

ECC relies on the difficulty of solving the ECDLP. The ECDLP states that when given a base point P and its result (after scalar multiplication), finding the scalar value should be very challenging. This fundamental fact is what a lot of cryptography relies on. Pretty neat, huh?

So, why do we use ECC? Because it offers several advantages compared to other cryptographic systems, including:

• Strong security with shorter key lengths (thus better UX)
• Faster computations afforded by ECCs operation efficiency

Bilinear Pairings

Okay, I lied. We have one more topic to cover, but it’ll be quick. Let’s take a look at bilinear pairings. This one is gnarly and mostly beyond the scope of this post. But I want to give you an overview and refer you to other blog posts that explain it in more depth.

What are Bilinear Pairings?

Bilinear pairings establish relationships between elements in two distinct mathematical groups (such as two different finite fields). If we have three groups, $G_1$, $G_2$, and $G_t$ of prime order p, and $g_1$, $g_2$, and $g_t$ are the generators for each of these groups, then a bilinear map is a function:

In simpler terms, bilinear pairings allow us to do arithmetic (e.g., addition, multiplication, or exponentiation) on two elements from different groups and produce a result with specific mathematical properties.

The important property of bilinear pairings is “bilinearity.” This means for all u ∈ $G_1$, v ∈ $G_2$, and a, b ∈ $ℤ_p$:

This is useful because it makes it possible to do encrypted multiplication, as shown above. This is not possible in regular encryption, but the ability to do this makes ZKPs “succinct.” For a more in-depth explanation of bilinear pairings, you can read this and this.

Conclusion

Phew! Nice work. We covered a lot of ground here, and it’s ok if you didn’t grasp it all in one go. I encourage you to revisit this post several times to let it sink in.

Remember, if you have any questions, you can always reach me at @iam_preethi or preethi@zkcamp.xyz.